Measures of Dispersion

While measures of central tendency are used to estimate "normal" values of a dataset, measures of dispersion are important for describing the spread of the data, or its variation around a central value. Two distinct samples may have the same mean or median, but completely different levels of variability, or vice versa. A proper description of a set of data should include both of these characteristics. There are various methods that can be used to measure the dispersion of a dataset, each with its own set of advantages and disadvantages.

Range

• Defined as the difference between the largest and smallest sample values.
• One of the simplest measures of variability to calculate.
• Depends only on extreme values and provides no information about how the remaining data is distributed.

Example: Find the range of global observed sea surface temperatures at each grid point over the time period December 1981 to the present.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Air-Sea Interface" link. Select the NOAA NCEP EMC CMB GLOBAL Reyn_Smith dataset. Click on the "Reyn_SmithOIv2" link. Scroll down the page and select the "monthly" link under the Datasets and Variables subheading. Choose the "Sea Surface Temperature" link again located under the Datasets and Variables subheading. CHECK
Find Maximum Value	Click on the "Filters" link in the function bar. To the right, you will see a selection of grids from which you may select any one or combination. Select the Maximum over "T" command. CHECK EXPERT This operation finds the maximum SST for each grid point over the time grid T.
View Maximum Values	To see the results of this operation, choose the viewer window with land drawn in black. Maximum Observed Sea Surface Temperatures
Find Minimum Values and Subtract from Maximum Values	Return to the dataset page by clicking on the right-most link on the blue source bar. Click on the "Expert Mode" link in the function bar. Enter the following lines below the text already there: SOURCES .NOAA .NCEP .EMC .CMB .GLOBAL .Reyn_SmithOIv2 .monthly .sst [T]minover sub Press the OK button. CHECK The above command subtracts the monthly minimum SST from the monthly maximum SST. The result is a range of SST values for each spatial grid point.
View Range	To see your results, choose the viewer with land shaded in black. Range of Observed Sea Surface Temperatures Generally, there is a larger range of sea-surface temperatures near the coasts and in smaller, sheltered bodies of water compared to the open ocean. For example, the Caspian Sea has a sea surface temperature range of over 25°C, while the sea surface temperature range of the non-coastal Atlantic Ocean at a comparable latitude does not exceed 12°C. This image also illustrates relatively large ranges off the west coast of South America, which is related to the El Niño Southern Oscillation (ENSO).

Standard Deviation

• The standard deviation is the square root of the sample variance.
• Defined so that it can be used to make inferences about the population variance.
• Calculated using the formula:
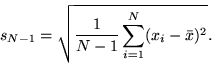
• The values computed in the squared term, x_i - xbar, are anomalies, which is discussed in another section.
• Not restricted to large sample datsets, compared to the root mean square anomaly discussed later in this section.
• Provides significant information into the distribution of data around the mean, approximating normality.
1. The mean ± one standard deviation contains approximately 68% of the measurements in the series.
   
2. The mean ± two standard deviations contains approximately 95% of the measurements in the series.
3. The mean ± three standard deviations contains approximately 99.7% of the measurements in the series.
• Climatologists often use standard deviations to help classify abnormal climatic conditions. The chart below describes the abnormality of a data value by how many standard deviations it is located away from the mean. The probablities in the third column assume the data is normally distributed.

Example: Calculate the standard deviation of monthly cloud cover over Equatorial Africa for January 1960 to December 1962.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Scroll down the page and select the UEA CRU New CRU05 dataset. Click on the "monthly" link. Select the "cloud cover" link under the Datasets and Variables subheading. CHECK
Select Temporal and Spatial Domains	Click on the "Data Selection" link in the function bar. Enter the text 25W to 50E, 40S to 38N, and Jan 1960 to Dec 1962 in the appropriate text boxes. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Calculate Standard Deviation Values	Click on the "Expert Mode" link in the function bar. Enter the following text below the text already there: dataflag [T]sum dup 1.0 sub div sqrt SOURCES .UEA .CRU .New .CRU05 .monthly .cld X (25W) (50E) RANGEEDGES T (Jan 1960) (Dec 1962) RANGEEDGES Y (40S) (38N) RANGEEDGES [T] rmsaover mul Press the OK button. CHECK The above commands calculate the standard deviation of the time series. The dataflag [T]sum commands determines, for each grid point, the number of non-missing elements in the time series. dup makes a copy of this number to then calculate n-1 using 1. sub (where n is the number of data points in time). The next step is to take n and divide it by n-1. The last step in the first line is to take the square root of n / (n-1). The following five lines of code reference the dataset being used, including the temporal and spatial ranges. The final two lines of code multiply the root mean square anomaly by the value calculated in the first line, sqrt(n / (n-1)).
View Standard Deviation Values	To see the results of this operation, choose the viewer window with coasts outlined. CHECK Standard Deviation of Monthly Cloud Cover Equatorial Africa exhibits low standard deviation values of monthly cloud cover compared to regions to its north and south. High standard deviation values correspond to areas with large interannual cloud cover variability. Note that the root mean square anomaly can be substituted for the standard devation if the sample size is sufficiently large. (Devore, Jay L. Probability and Statistics for Engineering and the Sciences. pp. 38-39, 259.)

Root Mean Square Anomaly / Root Mean Square

Root Mean Square Anomaly

• Also known as root mean square deviation.
• Very similar to standard devation, except used for large sample sizes (i.e., divisior is n instead of n-1) (Devore).
• RMSA calculated using the formula: 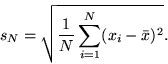, where xbar is the mean, x_i is each data value, and n is the number of observations.
• The term x_i – xbar is an anomaly, which is discussed in another section.
• Provides similar information into the dispersion of data as the standard deviation.
• Often used as a measurement of error.
• More commonly used than the standard deviation function in the statistical analysis of climate data because climate-related datasets are generally quite large in size, in terms of number of data points.

Root Mean Square

• Calculated using the formula:
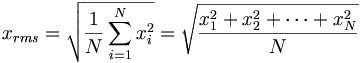
• Unlike the RMSA or standard deviation, The mean is not removed in the calculation.
• Acceptable to use only when dealing with large sample datasets (Devore).

Example: Calculate the root mean square anomaly of monthly cloud cover over Africa for January 1960 to December 1979.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Scroll down the page and select the UEA CRU New CRU05 dataset. Click on the "monthly" link. Click on the "cloud cover" link under the Datasets and Variables subheading. CHECK
Select Temporal and Spatial Domains	Click on the "Data Selection" link in the function bar. Enter the text 25W to 50E, 40S to 38N, and Jan 1960 to Dec 1979 in the appropriate text boxes. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Calculate Root Mean Square Anomaly	Click on the "Filters" link in the function bar. Select the RMSA over "T" command. CHECK EXPERT The result is a set of root mean square anomaly values (i.e. root mean square with mean removed). Higher (lower) values represent a larger (smaller) distribution of monthly cloud cover about the mean. *Note: Choosing the Root Mean Square over T instead of the Root Mean Square Anomaly over T will produce very different results. After completing the example, try going back and selecting the RMS over "T" command to see the difference between the two functions.
View Root Mean Square Values	To see the results of this operation, choose the viewer window with coasts outlined. CHECK Root Mean Square Anomaly of Monthly Cloud Cover Relatively low root mean square anomaly (RMSA) values are found in Equatorial Africa while regions to the north and south possess higher values. High RMSA values correspond to areas with large interannual cloud cover variability.

Interquartile Range (IQR)

• Calculated by taking the difference between the upper and lower quartiles (the 25th percentile subtracted from the 75th percentile).
• A good indicator of the spread in the center region of the data.
• Relatively easy to compute.
• More resistant to extreme values than the range.
• Doesn't incorporate all of the data in the sample, compared to the median absolute deviation discussed later in the section.
• Also called the fourth-spread.

Example: Find the interquartile range of climatological monthly precipitation in South America for January 1970 to December 2003.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Select the NASA GPCP V2 dataset. Select the "multi-satellite" link under the Datasets and Variables subheading. Select the "precipitation" link again under the Datasets and Variables subheading. CHECK
Select Temporal and Spatial Domains	Click on the "Data Selection" link in the function bar. Enter the text 90W to 30W, 60S to 10N, and Jan 1970 to Dec 2003 in the appropriate text boxes. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Compute Monthly Climatologies	Select the "Filters" link in the function bar. Choose the Monthly Climatology command. CHECK EXPERT This command computes the average cloud cover over all years for each month, January through December (i.e. climatological monthly cloud covers).
Calculate Interquartile Range	Enter into Expert Mode. Enter the following lines under the text already there: [T]0.25 0.75 0 replacebypercentile [percentile]differences Press the OK button. CHECK The replacebypercentile calculates the upper and lower quartiles for each grid point in the spatial field over the January to December climatologies. The differences command then takes the difference of the two values along the percentile grid. The result is a dataset of interquartile ranges at each grid point in the spatial field.
View Interquartile Range	To see the results of this operation, choose the viewer window with coasts outlined. CHECK Interquartile Range of Climatological Monthly Precipitation The higher the interquartile range, the more variability in the data. The Amazon Basin exhibits high intraannual precipitation variability, while areas to the north and south exhibit lower precipitation variability.

Median Absolute Deviation (MAD)

• A more comprehensive alternative to the IQR by incorporating all of the data in the sample.
• MAD = median |X_i – q_.5| where X_i represents each value and q_.5 represents the median.
  

Example: Find the median absolute deviation of climatological monthly precipitation in South America for January 1970 to December 2003.

Locate Dataset and Variable	*NOTE: This example uses the same dataset and variable as the previous example. Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Select the NASA GPCP V2 dataset. Select the "multi-satellite" link under the Datasets and Variables subheading. Select the "precipitation" link again under the Datasets and Variables subheading. CHECK
Select Temporal and Spatial Domains	Click on the "Data Selection" link in the function bar. Enter the text 90W to 30W, 60S to 10N, and Jan 1970 to Dec 2003 in the appropriate text boxes. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Compute Monthly Climatologies	Select the "Filters" link in the function bar. Choose the Monthly Climatology command. CHECK EXPERT
Calculate Median Absolute Deviation	Enter Expert Mode via the function bar and enter the following lines under the text already there: SOURCES .NASA .GPCP .V2 .multi-satellite .prcp Y (60S) (10N) RANGEEDGES X (90W) (30W) RANGEEDGES T (Jan 1970) (Dec 2003) RANGEEDGES yearly-climatology [T] medianover sub Press the OK button. CHECK The above command computes the median value over the monthly climatologies at each grid point in the field. In Expert Mode, enter the command: abs Click the OK button. CHECK This command takes the absolute value. Enter the command: [T] medianover Click the OK button. CHECK
View Median Absolute Deviation	To see the results of this operation, choose the viewer window with coasts outlined. CHECK Median Absolute Deviation of Climatological Monthly Precipitation The higher the median absolute deviation, the more variability in the data. Similar to the IQR example, the Amazon Basin exhibits high intraannual precipitation variability, while areas to the north and south exhibit lower precipitation variability.

Trimmed Variance

• Similar to variance, except that a proportion of the largest and smallest values in the dataset are ommitted before it is calculated.
• Less affected by outliers since the largest x% and the smallest x% of the sample are eliminated.
• Typical range for x% is 5% to 25%.
• Sometimes multiplied by an adjustment factor to make it more consistant with the ordinary sample variance. (Wilks, Daniel S. Statisical Methods in the Atmospheric Sciences. p 26).
• Analogous to the trimmed mean.

Example: Find the trimmed variance of average OLR values in the eastern United States for January 1980 to December 1999.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Cloud Characteristics and Radiation Budget" link. Select the NOAA NCEP CPC GLOBAL dataset. Click on the "monthly" link Select the "outgoing longwave radiation" link under the Datasets and Variables subheading. CHECK
Select Temporal and Spatial Domains	Click on the "Data Selection" link in the function bar. Enter the text 70W to 90W, 20N to 60N, and Jan 1980 to Dec 1999 in the appropriate text boxes. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Calculate Spatial Average	Click on the "Filters" link in the function bar. Select the Average over "XY" link. CHECK EXPERT This command takes a spatial average of the data.
Find Trimmed Variance	In Expert Mode, enter the command: [T] .2 0 replacebypercentile Click the OK button. CHECK The above command finds the 20th percentile of the data. The result is located under the Expert Mode text box in bold: 213.1339 W/m2. Make a note of this value. In the source bar, click on the [X Y] average box. This operation undoes the replacebypercentile command. Return to Expert Mode. Enter the following command under the text already there: [T] .8 0 replacebypercentile Click the OK button. CHECK This command finds the 80th percentile of the data. The result should be 237.7733 W/m2. Make a note of this value. In the source bar, click on the [X Y] average box. In Expert Mode, type in the command: 213 238 masknotrange Click the OK button. CHECK This command masks out all values not included in the indicated range. Click on the "Filters" link in the function bar. Choose RMSA over "T" CHECK EXPERT Since this dataset is large, we can assume that the root mean square is an acceptable estimate of the standard deviation. The value of the root mean square is 7.811205 W/m2. Calculate the trimmed variance by squaring the value above. In Expert Mode, enter the command: dup mul Click the OK button. CHECK The trimmed variance should be 61.01493 kg2s-6.