- Introduction
- Linear Interpolation
- Cressman Analysis
- Weaver Analysis
- Example: Interpolate Monthly Surface Temperature Data
- Example: Regrid Normalized Difference Vegetation Index Data for South America
Interpolation Techniques
Interpolation is the process of using known data values to estimate unknown data values. Various interpolation techniques are often used in the atmospheric sciences. One of the simplest methods, linear interpolation, requires knowledge of two points and the constant rate of change between them. With this information, you may interpolate values anywhere between those two points. More sophisticated interpolations are also available in the Data Library. They are often applied to station datasets with irregular spacing between stations. The Cressman and Weaver analysis interpolation techniques are covered in this tutorial section. Both methods are primarily used to estimate equally-spaced latitude / longitude grid data from station data or gridded data with non-constant spacing.
Linear Interpolation
Linear interpolation is a simple technique used to estimate unknown values that lie between known values. The concept of linear interpolation relies on the assumption that the rate of change between the known values is constant and can be calculated from these values using a simple slope formula. Then, an unknown value between the two known points can be calculated using one of the points and the rate of change. Linear interpolation is a relatively straightforward method, but is often not sophisticated enough to effectively interpolate station data to an even grid. Linear interpolation is often used to regrid evenly-spaced data, such as longitude / latitude gridded data, to a higher or lower resolution.
Example: Regrid NOAA NCDC GCPS Monthly Gridded Precipitation Anomalies for Europe from a 5° x 5° resolution to a 1° x 1° resolution.| Locate Dataset and Variable |
|
| Select Temporal and Spatial Domains |
|
| View Gridded Data at a 5° x 5° Resolution |


|
| Perform Linear Interpolation |
|
| View Results at a 1° x 1° Resolution |


|
Cressman Analysis
George Cressman developed the Cressman interpolation technique in 1959. The technique interpolates station data to a user-defined latitude-longitude grid. Multiple passes are made through the grid at consecutively smaller radii of influence to increase precision. The radius of influence is defined as the maximum radius from a grid point to a station by which the observed station value may be weighted to estimate the value at the grid point. Stations beyond the radius of influence have no bearing on a grid point value. At each pass, a new value is calculated for each grid point based on its correction factor. This correction factor is determined by analyzing each station within the radius of influence. For each such station, an error is defined as the difference between the station value and a value arrived by interpolation from the grid to that station. A distance-weighted formula (shown below) is then applied to all such errors within the radius of influence of the grid point to arrive at a correction value for that grid point. The correction factors are applied to all grid points before the next pass is made. Observations nearest the grid point carry the most weight. As the distance increases, the observations carry less weight. The cressman function in Ingrid calculates the weights as follows:W = (R2 - r2)/(R2 + r2)
where R = influence radius and r = distance between the station and the gridpoint. The weighting function is pictured below.
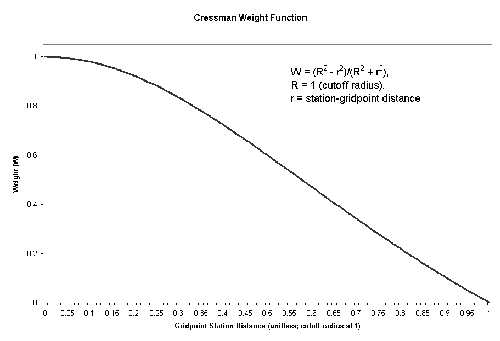
As the radius of influence is tightened, results become more representative of the observed data. The analysis value at each gridpoint is calculated as the analysis value from the previous pass added to the sum of the products of the calculated weights and the difference between the actual station value and the interpolated background value at the station, divided by the sum of the weights. The Data Library performs three passes by default, at 4, 2.5, and 1.5. These numbers are proportions of the average minimum station distance calculated in the function. These parameters may be changed when entering the command in Ingrid. There is also a minimum station number parameter, which ensures a certain number of station data points must be included within the radius of influence for an analysis value to be calculated for that gridpoint. If the minimum station number requirement is not met for a given gridpoint, a missing value will be assigned.
Cressman schemes may be used with data assimilation as well. Data assimilation is the analytical process of incorporating an estimation of the state of the atmosphere into a numerical model. By the early 1960s, weather centers within the United States began using data assimilation methods to improve forecasting techniques. They used interpolation techniques, such as the Cressman analysis, to interpolate current atmospheric conditions onto an evenly spaced grid. The Cressman analysis assigns weighted values of the observed stations to the model initialization, similar to the interpolation technique described above. However, Cressman suggests that persistence (climatology) values can be assigned if there are an insufficient number of stations in the area.
Advantages
- Simple and computationally fast (speed depends upon the number of scans).
- Generally more accurate than other simple methods such as linear interpolation.
- Can be unstable if grid density is higher than station density (i.e., more grid points than station data points).
- Sensitive to observational errors (random observation errors can generate unphysical features in analysis).
- Analysis may produce unrealistic extrema in the grid values, especially near the edges of the spatial domain.
- Does not account for the distribution of observations relative to each other.
- Consistency of the result with observations varies with observation (station) density.
- Optimum radii of influence have to be determined by trial and error.
Example: Perform a Cressman analysis of monthly surface temperature anomaly data over Australia for December 2000.
| Locate Dataset and Variable |
|
| Select Stations In Australia and Surrounding Islands |
|
| Select Stations With 30-Year Climatology |
|
| Compute Anomalies |
|
| Select Temporal Domain |
|
| Perform Cressman Analysis |
|
| View Results |


|
| Generate Colormap |
|
| View Results with New Color Scheme |


|
Weaver Analysis
The Weaver analysis is another type of interpolation scheme, developed at the Climate Prediction Center in the 1970's. In the Data Library, a simplified weaver function can be used to perform unweighted interpolation, examples of which are shown below. Weaver analysis is different from the Cressman analysis in many ways. First, the Weaver analysis does not use radii of influence. When the weaver function is used to interpolate to an equally spaced longitude/latitude grid, only the observations located within each grid box are used to calculate the interpolated value for that grid box. Any observations located outside the grid box, regardless of their proximity to the boundary of the grid box, will not affect the interpolated value of the grid box. Second, the weaver function does not weight the values of the observations. The value of each grid box is found by computing a simple arithmetic average of the observations.
Advantages- Simple and fast (speed depends upon the resolution of the grid).
- Generally more accurate than other simpler methods such as linear interpolation.
- Avoids unrealistic, extreme values at the edges of the domain.
- Spatial resolution is increased at the expense of missing data, and vice versa.
- As the resolution decreases (i.e., number of stations per grid box increases), extreme observations generally have less impact on the interpolated values.
- As the resolution increases (i.e., number of stations per grid box decreases), more grid boxes will not contain at least one station, and will therefore be identified as missing.
- Ignores the influence of stations outside each grid box.
- Potential errors enhanced at very low spatial resolutions and when using datasets with low station density.
| Locate Dataset and Variable |
*NOTE: This example uses the same dataset and variable as the previous example.
|
| Select Stations In Australia and Surrounding Islands |
|
| Select Stations With 30-Year Climatology |
|
| Compute Anomalies |
|
| Select Temporal Domain |
|
| Perform Weaver Analysis |
|
| Generate Colormap |
|
| View Results |


|
| Perform Weaver Analysis at a 5° Resolution |
|
| View Results |


|
| Locate Dataset and Variable |
|
| Select Domains |
|
| Perform Weaver Interpolation |
|
| View Results |


|